Seznam úloh k projektům

Jednoduchá konzolová aplikace

Matematické cvičení

Zadání

Cílem je implementovat jednoduchý kalkulátor, který bude umět sčítat číslice v různých soustavách.

Specifikace vstupu

Na vstupu je několik bloků. Každý blok mimo posledního začíná řádkem s kladným celým číslem z (toto číslo je menší než 35), poslední blok začíná nulou a nemá být zpracováván. Na druhém řádku každého bloku se nachází dvě nezáporná čísla x a y oddělená mezerou, která jsou zapsána standardním způsobem v soustavě o základu z. U soustav o základu větším než 10 se pro cifry s hodnotou větší než 9 používá písmen A, B.... Pokud má soustava základ jedna, používá se pouze cifra jedna a a počet cifer je roven velikosti čísla (viz vzorový výstup); nula se v jedničkové soustavě zapisuje jako jednociferné číslo, jediná cifra 0. Čísla, která váš program obdrží na vstupu, nebudou na svém začátku obsahovat přebytečné nuly. Čísla mají nejvýše 1000 cifer.

Specifikace výstupu

Výstup má obsahovat pro každý blok na vstupu jeden řádek. Na řádku mají být vypsána čísla x a y oddělená mezerou, znakem + a mezerou. Za nimi má následovat mezera, znak =, mezera a číslo x+y. Všechna čísla mají být zapsána standardním způsobem v soustavě o základu z.

Příklad vstupu a výstupu

16
A0 FE
1
1111 11
0

A0 + FE = 19E
1111 + 11 = 111111

Testování obrázků

Zadání

Cílem je implementovat jednoduchý analyzátor obrázků, který poprovná dva obrázky a zjistí, v jakém vztahu k sobě jsou. Může nastat jeden z těchto případů:

• shoda
• otočení o 90^o po směru hodinových ručiček
• otočení o 180^o po směru hodinových ručiček
• otočení o 270^o po směru hodinových ručiček
• zrcadlení podle horizontální osy
• zrcadlení následované otočením (podle pořadí výąe)

Specifikace vstupu

První řádek vstupu je celé číslo N, udávající počet zadání. Dále následují jednotlivá zadání. Každé zadání se skládá z řádky o jednom čísle R (2<=R<=10) udávajícím velikost vzoru a R řádků. Každý řádek obsahuje R znaků '.' (tečka) nebo 'x' (řádek původního vzoru), mezeru a druhých R teček a 'x'ek (řádek transformovaného vzoru).

Specifikace výstupu

Pro každé zadání vypište jednu řádku obsahující jednu z těchto odpovědí: 'Shoda', 'Otoceni o X stupnu', kde X je '90', '180' nebo '270', 'Zrcadleni', 'Zrcadleni a otoceni o X stupnu', případně 'Ruzne vzory'.

Příklad vstupu a výstupu

Vstup:

4
5
x...x ....x
.x... ...x.
...x. .x...
..x.x ..x..
....x xx..x
2
x. xx
x. xx
4
..x. ...x
xx.. ....
.... xx..
...x ..x.
4
.x.. ..x.
.x.x x...
.... ..xx
..x. ....

Otoceni o 90 stupnu
Ruzne vzory
Zrcadleni
Zrcadleni a otoceni o 270 stupnu

Anagramy

Zadání

K zadanému slovu vypište všechny jeho anagramy. Anagram je katové slovo, které vznikne přeuspořádáním písmen z původního slova. Každé slovo na výstupu bude právě jednou a všechna slova budou setříděna podle abecedy sestupně (od a do z). Ve vstupním slově, jehož anagramy budete generovat, se mohou některé symboly opakovat.

Specifikace vstupu

Na prvním řádku je číslo N. To udává, kolik řádku následuje. Na následujících N řádcích je N slov, každé na samostatném řádku.

Specifikace výstupu

Ke každému slovu ze vstupu vygenerujte všechny jeho anagramy (včetně původního slova) setříděné sestupně podle abecedy. Slova se mohou skládat z malých a velkých písmen anglické abecedy.

Příklad vstupu a výstupu

Vstup:

3
aAb
abc
acba

Aab
Aba
aAb
abA
bAa
baA
abc
acb
bac
bca
cab
cba
aabc
aacb
abac
abca
acab
acba
baac
baca
bcaa
caab
caba
cbaa

Převod na zlomek

Zadání

Všechna racionální čísla lze vyjádřit ve tvaru p/q. Kde p a q jsou přirozená čísla. Pokud bychom ovšem chtěli vyjádřit například 7/22 v podobě reálného čísla budou se něktéré číslice "nekonečně krát" opakovat (7/22 = 0.318181818...).
Vaším ukolem bude pro číslo s opakující se reálnou částí najít původní zlomek. Pro čísla menší než jedna můžete využít následující výraz:

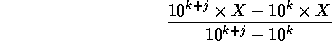
Kde k je počet neopakujících se číslic, a j je počet opakujících se číslic. X je původní číslo jehož zlomkovou reprezentaci hledáne.
Pro předchozí příklad bychom získlali: X = 0.318, k = 1, j = 2. Po dosazení do uvedeného výrazu bychom získali: 318.1818... - 3.18 / 1000 - 10, po upravách to je 315 / 990 respektive 7 / 22.

Specifikace vstupu

Na prvním řádku je číslo N toto číslo udává počet zadání, které následují. Každé zadání obsahuje dva čísla. První číslo reprezentuje počet opakujících se míst a druhé je reálné číslo X, jehož zlomkovou reprezentaci se snažíme najít. X bude větší než nula a menší než jedna. Počet opakujících se číslic a neopakujících se číslic u žádného čísla nebude větší než 10.

Specifikace výstupu

Pro každé zadání vytiskněte původní zlomek p / q, jehož vyčíslením vzniklo číslo X. Zlomek musí být normalizován do tvaru, kdy čitatel a jmenovatel nemají žádného společného dělitele kromě jedné.

Příklad vstupu a výstupu

Vstup:

4
2 0.318
1 0.3
2 0.09
6 0.714285

7/22
1/3
1/11
5/7

Vyčísli zlomek

Zadání

Racionální čísla lze zadat v podobě zlomku jako p / q. Některá takto zadaná čísla ovšem nelze vyšíslit a zapsat, protože kdybychom dělili p číslem q, poslední část reálné části čísla se opakuje do nekonečna. Například číslo 1/3 je 0.333333... . Vaším úkolem je pro dané čísla p a q najít p/q a vypsat toto číslo. V tomto problému předpokládejte, že opakující se části je první řetězec minimální delky na pravé straně čísla. Například pro číslo 1/3 (0.3...) to bude 3 na první pozici. Pro číslo 1/250 (0.0040...) to bude 0 na čtvrté pozici.

Specifikace vstupu

První řádek vstupu reprezentuje číslo N. Toto číslo udává počet zadání. Na dalších N řádcích jsou jednotlivá zadání. Jde o čísla p a q. p/q budete počítat. Čísla na vstupu budou menší než 3000.

Specifikace výstupu

Pro každé zadání ze vstupu vytiskněte p/q. Na výstup vytiskněte výsledek a to tak, že část okakující se do nekonečna uzavřete do závorek. Pokud by číslo mělo za desetinnou tečkou víde než 50 znaků, vytiskněte jen 50 číslic za desetinnou tečkou a místo zbytku vytiskněte "...)". Předpokládejte, že u všech číslic na vstupu začne opakujíc se část do padesáte číslice. Pod samotné číslo vytiskněte počet číslic v opakující se části dle ukázkového vstupu a za každé zadání vytiskněte prázdný řádek.

Příklad vstupu a výstupu

Vstup:

3
76 25
5 43
1 397

76/25 = 3.04(0)
Pocet opakujicich se cisel: 1

5/43 = 0.(116279069767441860465)
Pocet opakujicich se cisel: 21

1/397 = 0.(00251889168765743073047858942065491183879093198992...)
Pocet opakujicich se cisel: 99

Šachovnice

Zadání

Vašim úkolem je přečíst obraz šachovnice a vypsat pozici figur v šachové notaci.

Specifikace vstupu

Vstup je tvořen ASCII obrazem šachovnice s vyznačenými pozicemi jednotlivých figur. Bíle figury jsou zapsány jako velká písmena, černá jako malá písmena. Jednotlivé figury jsou značeny následovně: "K" (King - král), "Q" (Queen - dáma), "R" (Rook - věž), "B" (Bishop - střelec), "N" (Knight - kůň), or "P" (Pawn - pěšec). Jednotlivá pole jsou znázorněna pomocí znaků plus ("+"), mínus ("-") a pipe ("|"). černá pole jsou vyplňěna pomocí dvojteček (":"), bílá pomocí teček (".").

Specifikace výstupu

Výstup je tvořen dvěma řádky. První obsahuje řetězec "White: " následovaný pozicemi bílých figur. Druhý obsahuje řetězec "Black: " následovaný pozicemi černých figur.

Pozice jednotlivých figur jsou odděleny pomocí čárky. Popis pozice je tvořen velkým písmenem, které určuje typ figury (kromě pěšcu, u kterých je vynechán). Tento znak je bezprostředně následován pozicí figury v standardní notaci - malé písmeno "a" - "h" určující sloupec ("a" je úplně v levo) a číslice mezi 1 a 8 určující řádek (8 je první řádek vstupu).

Figury musí být seřazeny v následujícím pořadí: Král("K"), Dáma ("Q"), Věž ("R"), Střelec ("B"), Kůň ("N"), and pěšci. Pokud se na šachovnici vyskytují dvě figury stejného typu, musí bílá figura s nižším číslem řádku být před bílou figurou s vyšším číslem řádku, a černá figura s vyšším číslem řádku před černou figurou s nižším číslem řádku. Pokud jsou v jednom řádku dvě stejné figury, budou vypsány v pořadí podle sloupců (od "a" k "h").

Příklad vstupu a výstupu

Vstup:

+---+---+---+---+---+---+---+---+
|.r.|:::|.b.|:q:|.k.|:::|.n.|:r:|
+---+---+---+---+---+---+---+---+
|:p:|.p.|:p:|.p.|:p:|.p.|:::|.p.|
+---+---+---+---+---+---+---+---+
|...|:::|.n.|:::|...|:::|...|:p:|
+---+---+---+---+---+---+---+---+
|:::|...|:::|...|:::|...|:::|...|
+---+---+---+---+---+---+---+---+
|...|:::|...|:::|.P.|:::|...|:::|
+---+---+---+---+---+---+---+---+
|:P:|...|:::|...|:::|...|:::|...|
+---+---+---+---+---+---+---+---+
|.P.|:::|.P.|:P:|...|:P:|.P.|:P:|
+---+---+---+---+---+---+---+---+
|:R:|.N.|:B:|.Q.|:K:|.B.|:::|.R.|
+---+---+---+---+---+---+---+---+

White: Ke1,Qd1,Ra1,Rh1,Bc1,Bf1,Nb1,a2,c2,d2,f2,g2,h2,a3,e4
Black: Ke8,Qd8,Ra8,Rh8,Bc8,Ng8,Nc6,a7,b7,c7,d7,e7,f7,h7,h6

Šachy

Zadání

Hodnost matice

Zadání

Aplikace na zjištění hodnosti matice. Vstupem bude libovolná matice a výstupem bude číslo, které představuje hodnost matice. Meziřešením je převod zadané matice na trojúhelníkový tvar.

Specifikace vstupu

První řádek vstupu je celé číslo M, udávající počet zadání řádků v matici. Další řádek obsahuje číslo N reprezentující počet sloupců matice. Následuje m řádků matice, přičemž každý řádek obsahuje n reálných čísel.

Specifikace výstupu

Na konzoli se vypíše text "Hodnost matice je" + hodnost matice (=kladné celé číslo).

Příklad vstupu a výstupu

Vstup:

3
3
333
222
111

Hodnost matice je 1.

Palindromy s čísly

Zadání

Například:
195 Počáteční hodnota
591
-----
786
687
-----
1473
3741
-----
5214
4125
-----
9339 Výsledný palindrom.

V tomto konkrétním příkladě jsme nalezli palindrom (číslo 9339) ve čtvrtém kroku výpočtu.

Specifikace vstupu

První řádek vstupu je celé číslo M, udávající počet zadání. Každé zadání je jedno číslo. Z tohoto čísla se pokusíte získat palindrom použitím metody popsané výše.

Specifikace výstupu

Pro každé zadání se na výstup vypíše řádek obsahující celá čísla X a Y odělená mezerou. Číslo X udává počet kroků potřebných k vytvoření palindormu a číslo Y vytvořený palindrom. Pokud by při výpočtu číslo přesáhlo celočíselny typ int a nebo počet kroků při výpočtu byl větší než 1000, vypište místo dvojice X a Y text: NENALEZENO.

Příklad vstupu a výstupu

Vstup:

3
195
265
750

4 9339
5 45254
3 6666

Rozklad na prvočísla

Zadání

Implementujte algoritmus, který najde rozklad čísla na jeho prvočíselné dělitele. Pokud by například bylo na vstupu číslo 195, pak jeho rozkladem na prvočíselné dělitele je sekvence (3,5,13). Pak platí: 195 = 3 * 5 * 13.

Specifikace vstupu

Na vstupu bude sekvence čísel. Pro každé číslo vytiskněte jeho prvočíselný rozklad. Sekvence čísel bude ukončena číslem 0. Pokud na vstupu narazíte na toto číslo, můžete vykonávání ukončit. Všechna čísla budou v rozmezí od -1 000 000 000 do 1 000 000 000.

Specifikace výstupu

Pro každé číslo vytiskněte na jeden řádek řetězec obsahující: ono číslo, rovnítko, jeho rozklad. V rozkladu jsou vypsáni všichni prvočíselní dělitelé. Tito dělitelé jsou oddělení znakem: x. pokud je číslo záporné, bude vypsáno při rozkladu i číslo -1, jinak jednička v seznamu dělitelů nebude. Pro přehlednost budou navíc všechny elementy na výstupu odděleny mezerami.

Příklad vstupu a výstupu

Vstup:

-190
-191
-192
-193
-194
195
196
197
198
199
200
0

-190 = -1 x 2 x 5 x 19
-191 = -1 x 191
-192 = -1 x 2 x 2 x 2 x 2 x 2 x 2 x 3
-193 = -1 x 193
-194 = -1 x 2 x 97
195 = 3 x 5 x 13
196 = 2 x 2 x 7 x 7
197 = 197
198 = 2 x 3 x 3 x 11
199 = 199
200 = 2 x 2 x 2 x 5 x 5

Nejkratší cesta v orientovaném grafu

Zadání

Vytvořte program, který najde nejkratší cestu v orientovaném ohodnoceném grafu. Vstupem programu bude definice grafu. Graf obsahuje orientované hrany. Tyto hrany jsou ohodnoceny celým nenulovým číslem. Výstupem pak bude nejratší cesta mezi dvěmi zadanými vrcholy. Program čte vstupní data ze standardního vstupu a výsledky zapisuje na standardní výstup.

Specifikace vstupu

Vstup se skládá ze Z zadání. První řádek vstupu obsahuje právě jedno celé kladné číslo Z. Dále následují jednotlivá zadání. Každé zadání je tvořeno následujícími údaji:

• První řádek obsahuje kladné celé číslo N označující počet vrcholů grafu. Vrcholy jsou číslovány od 0 do N-1.
• Další řádek obsahuje číslo M udávající počet hran v grafu.
• Následuje M řádků obsahující popisy jednotlivých hran. Každá hrana je reprezentovaná trojicí X Y C. Kde X a Y jsou čísla z internalu <0,N-1> a reprezentují počáteční (X) a cílový (Y) vrchol. C reprezentuje cenu této hrany. C je celé číslo větší než nula.
• Poslední řádek zadání obsahuje dva čísla A a B. Oba patří do intervalu <0,N-1>. Jde o specifikaci počátečního (A) a konečného (B) vrcholu.

Při čtení vstupních dat předpokládejte, že zadání neobsahuje žádné formální ani věcné chyby.

Specifikace výstupu

Pro každé zadání bude výstupem jedno celé číslo. Toto číslo bude cena nejkratší cesty mezi vrcholy A a B.

Příklad vstupu a výstupu

1
5
6
0 1 2
0 2 1
1 3 3
3 1 3
2 3 5
1 4 7
0 3 

5

Násobení čísel

Zadání

Cílem problému bude vypsat řešení násobení dvou čísel. Tyto čísla navíc musejí být vypsána včetně celého postupu řešení při násobení. Pokud například násobíme 123 číslem 95 měl by výpis vypadat takto:

    123
     95
    ---
    615
  1107
  -----
  11685

Specifikace vstupu

Každý řádek na vstupu (kromě posledního) bude obsahovat dvě čísla x a y. Poslední řádek obsahuje pouze jedno číslo a tím číslem bude číslo nula. Podle toho poznáte, že jde o konec vstupu. Čísla budou mít maximálně 10 číslic.

Specifikace výstupu

Pro každou dvojici číslic vytiskněte jejich násobení včetně celého postupu. Za každým násobením pak vytiskněte prázdný řádek. Čísla vytiskněte podle ukázkového výstupu. Budou platit tato pravidla.

• Pokud by v prostředí části (zachycující vlastní výpočet) bylo méně řádku než dva netiskněte tuto část a pouze vytiskěte výsledek.
• Číslo nula tiskněte pouze v případě, že má význam (tedy ve výsledku, ne u postupu).
• Počet - v prvním horizontální "čáře" bude stejný, jako u delšího z čísel x a y. Počet - u druhé oddělující čary (pokud bude tisknuta) bude stejný jako u výsledku.

Příklad vstupu a výstupu

Vstup:

   4 7
135  46
    12345   862
0 123456789
0

 4
 7
 -
28

 135
  46
 ---
 810
540
----
6210

   12345
     862
   -----
   24690
  74070
 98760
--------
10641390

        0
123456789
---------
        0

Kůň na šachovnici

Zadání

Vaším úkolem bude zjistit, kolik tahy lze minimálně posunout šachovou figuru označovanou jako kůň z místa A na šachovnici do místa B.

Specifikace vstupu

Vstup se bude skládat z několika zadání. Každé zadání bude na samostatném řádku. Každý řádek bude obsahovat aktuální pozice figury a cílová pozice figury. Obě pozice budou zadány ve standardní notaci. Písmeno udává první rozměr (sloupec šachovnice, a-h) následující číslice řádek šachovnice (1-8).

Specifikace výstupu

Pro každé zadání vytiskněte řetězec: "To get from xx to yy takes n knight moves.", kde xx je starovní pozice, yy cílová pozice a n po počet tahů.

Příklad vstupu a výstupu

Vstup:

e2 e4
a1 b2
b2 c3
a1 h8
a1 h7
h8 a1
b1 c3
f6 f6

To get from e2 to e4 takes 2 knight moves.
To get from a1 to b2 takes 4 knight moves.
To get from b2 to c3 takes 2 knight moves.
To get from a1 to h8 takes 6 knight moves.
To get from a1 to h7 takes 5 knight moves.
To get from h8 to a1 takes 6 knight moves.
To get from b1 to c3 takes 1 knight moves.
To get from f6 to f6 takes 0 knight moves.

Mince

Zadání

Předpokládejte, že máte 50, 25, 10, 5 a 1 korunové mince. Pokud jich máte nekonečně mnoho, kolika způsoby můžete sestavit daný obnos? Například 11 korun můžete sestavit jako 10ti koruna a koruna, nebo dvě pětikoruny a jedna koruna atd.

Specifikace vstupu

Vstup se skládá z N čísel. N sum, které máte spočítat.Každé číslo reprezentuje jedno zadání.

Specifikace výstupu

Pro každé zadání vytiskněte počet možných sestavení daného obnosu se zadaných pěti typů mincí. Váš program by měl úspěšně vyřešit úlohu až do 7000 korun.

Příklad vstupu a výstupu

Vstup:

11
26

4
13

Zadání

Vašim úkolem je napsat program, který spočítá obsah pracoúhelníku určeného jeho hranicí. Hranice je vždy uzavřená a probíhá po hranách čtvercové sítě (hranice mezi jednotlivými čtverečky). Můžete předpokládat, že se hranice nikde nekříží ani nedotýká.

Specifikace vstupu

První řádek obsahuje počet vstupů. Každý test, který následuje, tvoří 2 řádky. Na prvním jsou dvě celá čísla X a Y, která určují souřadnice počátečních bodů hranice. Na druhém řádku je řetězec popisující vlastní hranici. Každý znak představuje pohyb podél hranice o jednu jendotku. Povoleny jsou pouze znaky 'W' ("west - západ"), 'E' ("east - východ"), 'N' ("north - sever"), 'S' ("south - jih") a '.' ("Konec hranice", žádný pohyb). Znak ('.') je bezprostředně následován koncem řádku. Délka řádku nikdy nepřesáhne 100000 znaků.

Specifikace výstupu

Pro každý test bude výstup obsahovat jeden řádek obsahujícím text: "The area is XX squares." - místo znaků XX bude uveden obsah plochy rovnoběžníku.

Příklad vstupu a výstupu

Vstup:

1
2 1
EENNWNENWWWSSSES.

The area is 10 squares.

Římská čísla

Zadání

Ve středověku se často na stavbu umisťoval nápis, jehož zvýrazněná písmena tvořila římské číslo, které určovalo rok, kdy byla daná stavba postavena. Například budova s nápisem "My vsb is the best schooL In ostrava" byla určitě postavena v roce "MLI" tedy 1051. Avšak nápis byl často postupem času poškozen a proto nebylo možné určit, které znaky byly velké a tedy tvořily římské číslo. Pro tento případ bylo dohodnuto, že se za rok postavení bude brát poslední (tzn. největší) rok, který faný nápis představuje. Například u nápisu "my vsb is the best school in ostrava" je jasné že největším rokem je "MCLV" a tedy tato budova byla postavena v roce 1155.

Specifikace vstupu

Vstup se skládá z několika neprázdných řádků l₁,..., l_n. Každý z nich tvoří nápisy zapsané malými písmeny. Délka každého nápisu je nejvýše 10 000 znaků.

Specifikace výstupu

Pro každý vstupní řádek l_i je na výstup zapsáno jedno celé číslo. Toto číslo je nejvetší řimské číslo, které může být v nápisu l_i zakódováno, nebo 0, pokud nápis žádné řimské čislo neobsahuje.

Příklad vstupu a výstupu

Vstup:

my vsb is the best school in ostrava
no year

1155
0

Tranzitivní uzávěr grafu

Zadání

Vytvoření tranzitivního uzávěru v grafu (matice). Tranzitivní uzávěr orientovaného grafu je orientovaný graf s původními vrcholy a platí, že existuje hrana z uzlu U do uzlu V právě tehdy, když v původním orientovaném grafu existuje libovolná orientovaná cesta z uzlu U do uzlu V.

Specifikace vstupu

Vstup začíná číslem N. To udává počet zadání. Každé zadání začíná číslem M. To reprezentuje počet vrcholů v grafu. Vrcholy jsou číslovány od 0 do N-1. Následuje čtvercová matice, kde 1 znamená, že mezi uzlem daného řádku a sloupce existuje hrana. Pokud například na druhém řádku je jednička na pozici 3, znamená to že v grafu je hrana z vrcholu 1 (vrcholy jsou číslovány od nuly!) do vrcholu 2.

Specifikace výstupu

Výstupem je opět binární matice reprezentující výsledný graf, tranzitivní úzávěr.

Příklad vstupu a výstupu

Vstup:

1
6
101001
110000
011000
001110
000011
000011

111011
111011
111011
111111
000011
000011

Pozice

Zadání

Vaším úkolem bude určit pozici robota na hrací desce. Zadání specifikuje velkost hrací desky. Ta je obdelníková a skládá se s políček stejné velikosi. Následuje popis cesty robota. Robot se může otáčet a to vždy o devadesát stupňů buď v levo a nebo v pravo. Také může popojet o jedno pole ve směru, kterým je právě natočen. Vaším úkolem bude zjistit výslednou pozici robota na hrací desce, pokud znáte jeho startovní pozici a víte, jaké kroky postupně prováděl.

Specifikace vstupu

Vstup začíná dvěmi čísly X a Y (oba čísla budou menší než 100). Tyto čísla specifikují velikost hraci desky. Následuje několik popisů cesty robota. Každý popis cesty se skládá ze dvou řádků. První řádek obsahuje dvě souřadnice a aktuální natočení robota. Souřadnice jsou dva celá čísla. Souřadnice levého horního rohu hrací desky jsou 0,0. Následuje N,S,E,W. Tato značka odpovídá počátečnímu natočení robota (jde o anglické ekvivalenty světových stran). Pokud je robot natočen na Sever (North - N) a pohne se o jedno pole, jeho souřadnice (x,z) se změní na (x,y+1). Údaje na prvním řádku jsou odděleny mezerami. Druhý řádek obsahuje popis chování robota. Jde o sekvencí písmen:

• F - Forward - pohyb robota vpřed o jedno pole;
• R - Right - otočení robota do prava o 90 stupňů;
• L - Left - otočení robota do leva o 90 stupňů;

Specifikace výstupu

Pro každý popis cesty ze vstupu bude výstupem pozice a natočení po provedení všech popsaných kroků. Protože hrací plocha nemá mantinely, může se stát, že robot z hrací plochy spadne. V takovém případě vypište poslední pozici na hrací pološe a poznámku LOST. Vypisovaný popis pozice robota odpovídá svou strukturou popisu pozice na vstupu. Jednotlivé údaje jsou odděleny mezerou.

Více ukázkový vstup a výstup.

Příklad vstupu a výstupu

Vstup:

5 3
1 1 E
RFRFRFRF
3 2 N
FRRFLLFFRRFLL
0 3 W
LLFFFLFLFL

1 1 E
3 1 N
2 2 S

Cesta v bludišti

Zadání

Vytvořte program, který najde a zobrazí cestu v bludišti. Vstupem programu bude definice bludiště. Výstupem pak stejné bludiště s vyznačenou cestou mezi dvěma přesně specifikovanými body. Bludiště bude specifikováno v textovém formátu. Program čte vstupní data ze standardního vstupu a výsledky zapisuje na standardní výstup.

Specifikace vstupu

Vstup se skládá ze Z zadání. První řádek vstupu obsahuje právě jedno celé kladné číslo Z. Dále následují jednotlivá zadání. Každé zadání je tvořeno následujícími údaji:

• První řádek obsahuje dva kladné celé čísla N a M. Tyto čísla definují velikost bludiště. N udává počet řádku a M počet sloupců
• Dalších N řádků bude obsahovat právě M znaků. Přitom použité znaky mohou být:
  • # - reprezentující stěnu v bludišti. Cesta nemůže vést skrz stěnu ani mimo specifikované bludiště.
  • . - reprezentuje volné pole v bludišti. Cesta může vést skrz toto pole.
  • A - reprezentuje počátek cesty. Tento symbol bude v zadání právě jednou.
  • B - reprezentuje konec cesty. Tento symbol bude v zadání právě jednou.

Specifikace výstupu

Pro každé zadání bude výstupem N řádků obsahujících M znaků. Symboly ., #, A a B budou zkopírovány na výstup. Budou na stejné pozici jako byly na vstupu. V bludišti bude navíc vyznačená cesta z bodu A do bodu B a to pomocí znaku X. Protože se snažíme ušetřit, bude nalezena cesta optimální. Optimální cesta je taková, kde pro každý bod na cestě platí, že se dotýka jednou ze stran s předchozím a jednou ze stran s následující bodem na cestě. S žádným jiným bodem na cestě se nedotýká. Po každém bludišti bude vytištěn prázdný řádek.

Příklad vstupu a výstupu

Vstup:

2
5 5
A.#..
..#..
.....
..#..
..#.B
5 10
A.#.....#.
..#...#.#.
..#...#.#B
..#...#.#.
......#...

AX#..
.X#..
.XXX.
..#X.
..#XB

A.#..XXX#.
X.#..X#X#.
X.#..X#X#B
X.#..X#X#X
XXXXXX#XXX

Analyzátor obrazu

Zadání

Cílem úlohy je analyzovat obraz, na kterém se nachází několik kostek a zjistit, kolik na nich bylo hozeno.
Obraz kostek je značně zjednodušen. Obsahuje pouze tři typy bodů. Je to pozadí, kostka a tečka na kostce. Tyto body budou zadány pomocí znaků v textovém režimu.
O dvou bodech řekneme, že jsou sousedy pokud se dotýkají jednou ze stran. Pokud se dotýkají pouze rohy, sousedy nejsou.
Množina bodů S je souvislá, pokud pro každou dvojici bodů a,b v S platí, že existuje sekvence a1, a2, ... ak v S taková, že a = a1, b = ak, a pro každou dvojici ai a ai+1 platí, že jsou sousedy.
Maximální spojená oblast pak bude množnina bodů reprezentujících kostku či tečku na kostce, ke které nemůžeme přidat žádny bod (kromě bodů reprezentujících pozadí), který by byl sousedem nějakého bodu, který už v množině je.
Kostku pak lze definovat jako maximální spojenou oblast složenou z jiných bodů než jsou body reprezentující pozadí. Tečka na kostce pak je maximální oblast složená pouze ze znaků reprezentujících tečku na kostce.

Specifikace vstupu

Vstup se skládá z několika obrázků. Každý popis obrázku začíná řádkem, který obsahuje dva čísla X a Y. Ty reprezentují výšku (X) a šířku (Y) obrázku.
Následujících X řádku obsahuje právě Y znaků. Kde tečka (".") reprezentuje pozadí, hvězdička ("*") reprezentuje bod na kostce a "X" reprezentuje bod na tčece kostky. Každý obrázek bude obsahovat alespoň jednu kostku. Každá kostka bude mít od jedné do šesti teček. Maximální počet kostek je limitován jen velikostí obrázku. Kostky a tečky na nich mohou být různě veliké a mohou mít různé "tvary" (optické disproporce) a jsou brány jako jedna kostka, pokud jsou spojené.
Vstup je ukončen obrázkem, který má velikost 0 a 0. Ten už nebude zpracováván. Při čtení vstupních dat předpokládejte, že zadání neobsahuje žádné formální ani věcné chyby.

Specifikace výstupu

Pro každý obrázek vytiskněnte jeden řádek obsahující text "Hozeno:" následováný hody na kostkách na obrázku. Hody budou setřízeny vzestupně. Jednotlivé hody budou odděleny mezerou.

Příklad vstupu a výstupu

15 30
..............................
................*.............
...*****.......****...........
...*X***......**X***..........
...*****.....***X**...........
...***X*......****............
...*****........*.............
..............................
..............................
.....***.........******.......
....**X****......*X**X*.......
...*******.......******.......
..****X**........*X**X*.......
.....***.........******.......
..............................
3 3
...
XXX
...
0 0

Hozeno: 1 2 2 4
Hozeno: 1

Optimální násobení matic

Zadání

Pokud násobíme sekvenci matic, můžeme jednotlivá násobení provést v různém pořadí. Výsledek tato skutečnost neovlivní. Pokud nás ovšem zajímá, kolik elementárních ukonů násobení dvou čísel musíme provést, záleží na pořadí uzávorkování. Rozdílné uzávormování může změnit výsledný počet operací. Pokud bychom například měli matice A s rozměrem (10 x 20) a B (20 x 15) budeme muset při násobení A a B vynásobit 10 x 15 x 20 tedy 3000 čísel.
Pokud bychom měli matice X (5, 10), Y(10, 20), Z(20,35) můžeme provést:

Maximální suma

Zadání

Vaším úkolem bude najít v zadaném čtverci čísel obdelníkovou část, jejíž součet je maximální. Vybraná obdelníková část může být minimálně rozměru 1x2 a maximálně může pojímat všechna zadaná čísla. Pokud například je na vstupu čtverec čísel:

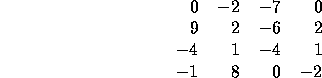
bude mít nejvetší součet obdelník velikosti 2x3 začínající na druhém řádku vlevo.

a součet všech jeho čísel bude 15.

Specifikace vstupu

Vstup bude začínat číslem N. Toto číslo reprezentuje počet zadání. Každé zadání začíná číslem X. Toto číslo je rozměr čtverce, ve kterém budete hledat maximální sumu. Pak následuje X * X čísel. Jde o čísla umístěná do čtverce. Začínají v levém horním rohu a pokračují zleva doprava a shora dolů.

Specifikace výstupu

Vytiskněte maximální součet souvislé obdelníkové oblasti v zadaném čtverci.

Příklad vstupu a výstupu

Vstup:

1
4
0 -2 -7  0 9  2 -6  2
-4  1 -4  1 -1
8  0 -2

15

Puzzle

Zadání

Váším cílem je v tomto problému ověřit, zda ze zadaných kostiček jde čí nejde sestavit puzzle. V našem případě mám sadu kostiček. Kostičky jsou všechny stejných rozměru. Kostičky mohou mít na stranách buď výstupek (jut) a nebo dutinu (cavity). Na stranách obrázku jsou kostičky rovné (flat). Příklad ukazuje následující obrázek.

Na vstupu bude rozměr puzzle a sada kostiček. Vaším úkolem bude vyřešit, zda jde z daných kostiček sestavit puzzle daného rozměru. Ve výsledném obrázku musí platit, že kostičky s rovnou stranou jsou jen na vnějším okraji obrázku. Pro každé dvě sousedící kostičky navíc platí, že pokud se dotýkají stranou má práve jedna z ních výstupek a druhá dutinu. Pro zjednodušení jsou navíc kostičky otočeny stejně, jak budou zadany na vstupu.

Specifikace vstupu

Na vstupu je několik zadání. Každé zadání začíná dvěmi čísly X a Y. Pokud jsou oba čísla rovna nule, jde o konec vstupu. Jinak čísla X a Y reprezentují rozměr výsledného obrázku. X i Y budou menší nebo rovny 6. Pro každé zadání pak následuje X * Y řádku. Na každém řádku bude popis jedné kostičky. Popis kostičky jsou 4 znaky z těchto prvků:

• F - reprezentuje rovnou stranu
• O - stranu s dutinou (cavity)
• I - stranu s výstupkem

Specifikace výstupu

Na výstu vypište ANO v případě, že ze zadaných kostiček lze složit puzzle specifikovaného rozměru a NE v případě, že nejde.

Příklad vstupu a výstupu

Vstup:

3 5
FOOF
FOOI
FOOI
FOOI
FFOI
IOOF
IOOI
IOOI
IOOI
IFOI
IOFF
IOFI
IOFI
IOFI
IFFI
0 0

ANO

Hanojské věže

Zadání

Máme tři kolíky označené čísly 1, 2 a 3. Na kolíky budeme navlékat kotouče opatřené dírkou uprostřed. Máme celkem N kotoučů, každý o jiném průměru. Na začátku jsou všechny kotouče na jednom kolíku seřazené od největšího po nejmenší tak, že největší je dole a nejmenší nahoře. Kolíky 2 a 3 jsou prázdné. Vašim úkolem je, přemístit všech N kotoučů na kolík 2 tak, aby byly opět stejně uspořádané. Při přenosu nesmí nikdy nastat situace, kdy by byl větší kotouč položen na menším.

Výrazy

Zadání

Vytvořte program, který vyčíslí zadaná aritmetický výraz. Výraz bude obsahovat čísla, operátory +, -, *, / a závorky s libovolným množstvím zanoření. Na vstupu program dostane několik aritmetických výrazů. Každý z nich vyčíslí a výsledek vypíše na výstup. V případě, že je zadaný výraz chybný, vypíše "Wrong expression.".

Příklad vstupu a výstupu

(65 - 3 * 5)/(2 + 3)
((65 - 3) * 5)/(2 + 3)
((64 - 3 * 5)/(2 + 3)

10
62
Wrong expression.

Logika

Zadání

Ověřte, zda je formule výrokové logiky splnitelná, je tautologií nebo je kontradikcí.

Specifikace vstupu

Na vstupu je číslo N udávající počet zadání. Každé zadání je na samostatném řádku a obsahuje formuli výrokové logiky s následující syntaxí:

• závorky ( )
• konjunkce &
• disjunkce v
• implikace >
• ekvivalence =
• negace ~

Specifikace výstupu

Na konzoli se vypíše text "Formule je: " + jedna z následujících kombinací:

• kontradikce
• splnitelná
• tautologie

Příklad vstupu a výstupu

Vstup:

1
( A & B ) > ~ ( ~ ( A & B ) )

Formule je tautologie.

Křížovka

Zadání

Křížovka může být uložena jako matice jedniček a nul. Nula reprezentuje bílý čtverec a jednička černý (bílé jsou pak určeny pro vpisování písmen). Vaším úkolem bude vypsat diagram popisující takto zadanou křížovku. Navíc máte zjisit, kolik slov bude v křížovce použito a očíslovat pole, kde bude začínat některé slovo. Slova budou do křížovky vpisována buď shora dolů, nebo zleva do prava ve vertikálním respektive horizontálním směru. Políčko je očíslováno (jde o pole kde začíná některé slovo) v případě, že jde o bíly čtvereček a:

1. čtvereček ihned pod daným polem je bíly a těsně nad ním není bíly čtvereček;
2. čtvereček ihned vpravo je bíly a čtvereček těsně vlevo od něj bílý není.

Ve vykresleném diagramu bude každý čtvereček reprezentován polem 4 x 6 znaků následujícím způsobem:

++++++                        ++++++         ++++++
++++++                        +nnn +         +    +
++++++                        +    +         +    +
++++++                        ++++++         ++++++

Kde první obazec definuje černý čtvereček, další dna bílý čtvereček. Znaky nnn reprezentují vepisovanou pozici. Pokud je černý čtvereček na okraji pole křížovky, nebude vypsán. Více demonstruje ukázkový vstup.

Specifikace vstupu

Vstup se skládá z několika zadání. Zadání začíná dvěmi čísly X a Y. Pokud jsou oba tato čísla nulová, jde o konec vstupu. V opačném případě jde o rozměr matice, která popisuje křížovku. Následuje X řádku obsahujících Y jedniček nebo nul. Jedničky a nuly popisují hrací pole křížovky dle pravidel popsaných výše.

Specifikace výstupu

Výstupem je diagram popisující křížovku včetně vyznačených pozic pro slova. Jednotlivá zadání budou oddělena prázdným řádkem.

Příklad vstupu a výstupu

Vstup:

6 7
1 0 0 0 0 1 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 1 0 0 1 1 1
0 0 0 1 0 0 0
1 0 0 0 0 0 1
5 3
1 0 1
0 0 0
1 1 1
0 0 0
1 0 1
0 0

     +++++++++++++++++++++
     +001 +    +002 +003 +
     +    +    +    +    +
++++++++++++++++++++++++++++++++++++
+004 +    ++++++005 +    +006 +007 +
+    +    ++++++    +    +    +    +
++++++++++++++++++++++++++++++++++++
+008 +    +009 +    +    +010 +    +
+    +    +    +    +    +    +    +
+++++++++++++++++++++    +++++++++++
+    ++++++011 +    +
+    ++++++    +    +
++++++++++++++++++++++++++++++++++++
+012 +013 +    ++++++014 +015 +    +
+    +    +    ++++++    +    +    +
++++++++++++++++++++++++++++++++++++
     +016 +    +    +    +    +
     +    +    +    +    +    +
     ++++++++++++++++++++++++++

     ++++++
     +001 +
     +    +
++++++++++++++++
+002 +    +    +
+    +    +    +
++++++++++++++++


++++++++++++++++
+003 +004 +    +
+    +    +    +
++++++++++++++++
     +    +
     +    +
     ++++++

Jednoduchý webový server

Databáze CD

Chat

Síťové šachy

Kontrolor souborů

Komprese

Vyhledávání souborů

Piškvorky

Komprese II

Grafický kalkulátor

Hra miny

Pexeso

Práce s tiskárnou

Elektronický diář

Provnávání souboru

Kreslítko

Dohled sítě

Painbrush